
Problem
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Example 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1
Constraints:
- 1 <= nums.length <= 104
- -104 < nums[i], target < 104
- All the integers in nums are unique.
- nums is sorted in ascending order.
target이라는 숫자가 주어지면 ascending order로 정렬된 array에서 몇번째 index에 그 값이 있는지를 찾는 문제!
Solution
Approach 1: Brute force
그냥 단순하게 생각해서 for문을 돌면서 target과 같은 값이 있는지 확인하고 같으면 그 index를 return한다.
이 풀이법은 O(n)이다. 0...nums.size-1까지 n번을 돌아야 index를 찾을 수 있기 때문이다
class Solution {
fun search(nums: IntArray, target: Int): Int {
for(i in 0..nums.size-1)
{
if(nums[i] == target) return i
}
return -1
}
}
Approach 2: Binary Search
좀 더 스마트하게 찾는 방법은 없을까?!
예전에 up&down 게임을 해본다고 가정해보자!
0~100까지 숫자중에 만약에 75를 찾는다고 해보자.
보통 본능적으로 우리는 50을 부르고 시작한다 ㅋㅋ 이 것은 일단 반절을 불러서 범위를 줄이고자 함이다.
이것이 바로 binary search의 원리이다.
50을 부르면 바로 up이 되고 우리는 0~50까지는 더이상 번호를 부를 필요가 없다.
왜냐하면 0~50에는 더이상 우리가 원하는 숫자가 없다. 50보다 up이기 때문이다.
계속 게임을 진행해보자.
여기서 만약에 50~100의 값의 중간 값인 75를 부르면 바로 우리는 2번만에 값을 찾는 행운을 얻었다!
0부터 쭉 숫자를 불렀다면 우리는 76번만에 숫자를 찾았겠지만(O(n))
binary search를 사용하면 O(logn)만에 찾을 수 있다.
그럼 Binary search에 대해 자세히 알아보자.
Intuition
Binary search 는 대상 값을 배열의 중간 요소와 비교하는 아이디어에 기반한 교과서적인 알고리즘이다.
목표 값이 중간 요소와 같으면 완료
목표 값이 더 작은 경우 왼쪽에서 계속 검색 (up&down게임에서 down을 하는 것과 동일)
목표 값이 더 크면 오른쪽에서 계속 검색 (up&down게임에서 up을 하는 것과 동일)
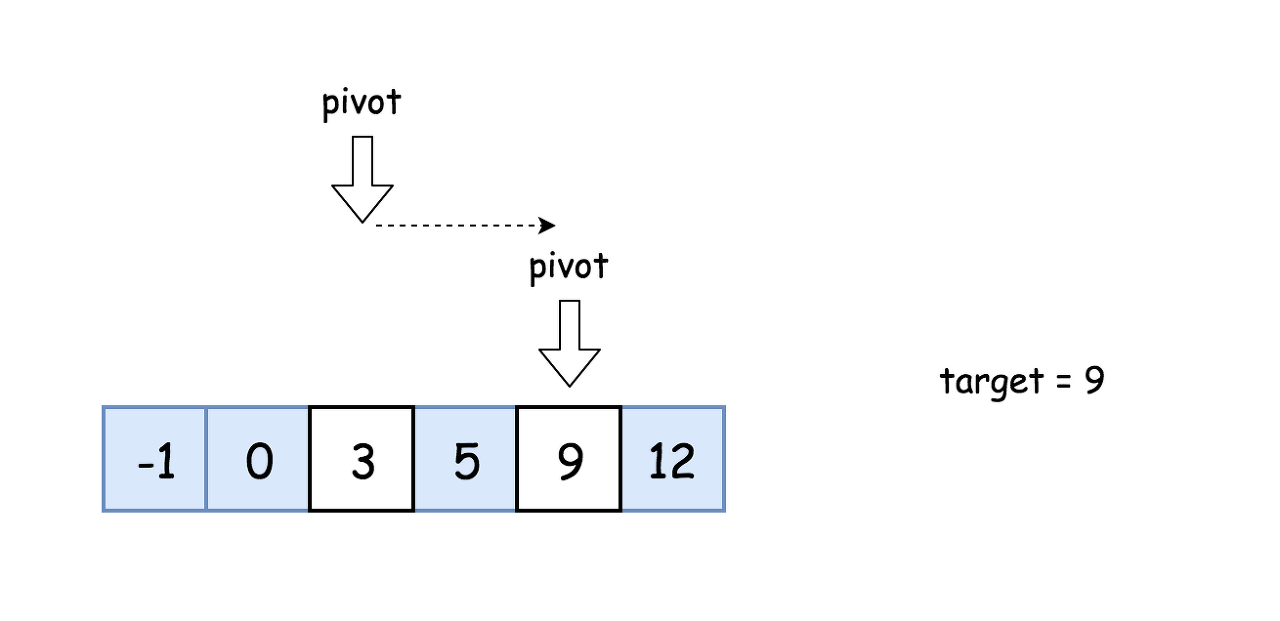
Algorithm
- 왼쪽 및 오른쪽의 index를 가르킬 포인터 초기화 : left = 0, right = n - 1. (up&down 게임에서 0~100까지 숫자를 맞추는 거라고 가정할 때 left는 0, right는 100이된다)
- While left <= right :
- 배열 nums[pivot]의 중간요소를 대상 값 target과 비교
- 중간 요소가 target과 같은 경우 target = nums[pivot] : return pivot.
- 대상을 아직 찾지 못한 경우 :
- If target < nums[pivot], 왼쪽에서 계속 검색 right = pivot - 1
- target이 nums[pivot]보다 작으면 right를 현재 pivot보다 1작은 곳으로 변경 pivot 후까지 검색할 필요가 없음
- Else 오른쪽에서 계속 검색 left = pivot + 1
- target이 nums[pivot]보다 크면 left를 현재 pivot보다 1 큰 곳으로 변경 pivot 전까지 검색할 필요가 없음
- If target < nums[pivot], 왼쪽에서 계속 검색 right = pivot - 1
- 배열 nums[pivot]의 중간요소를 대상 값 target과 비교
- Binary Search를 사용하려면 배열이 반드시 sorting되어 있어야 한다!
Implementation
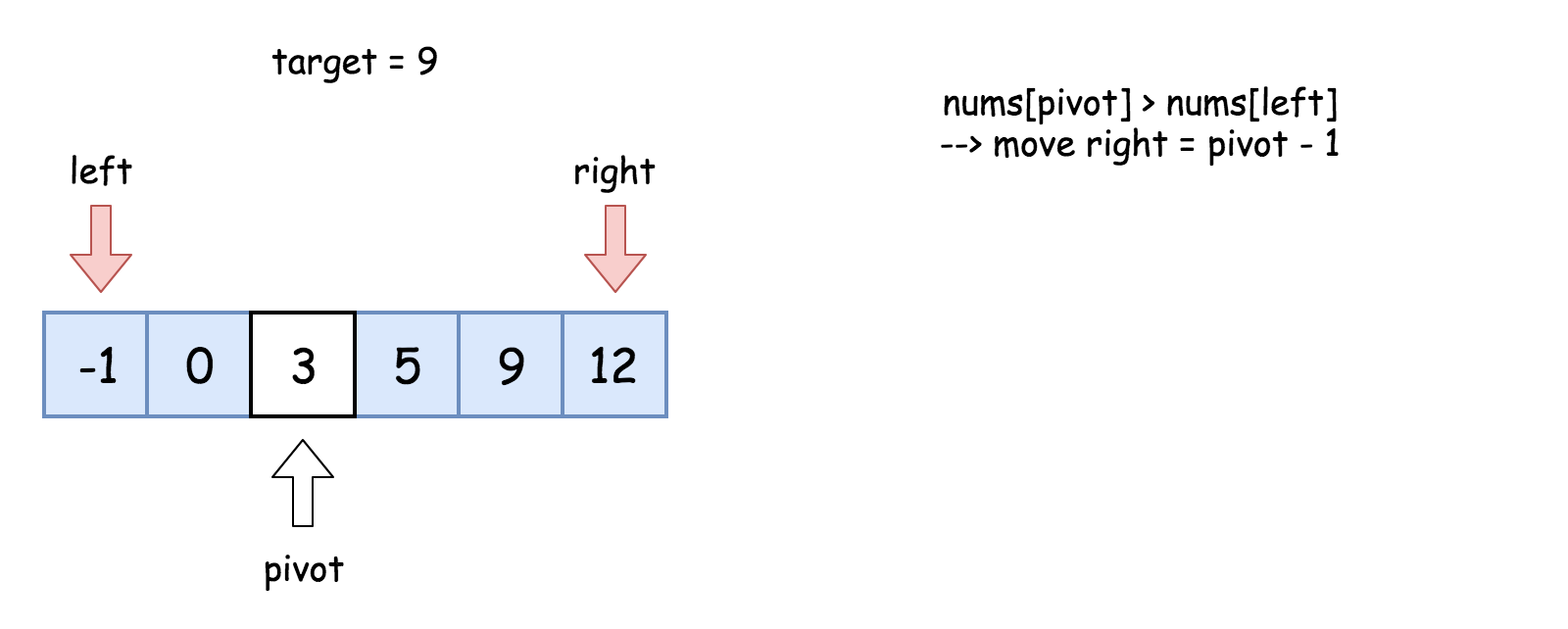
mid가 pivot이라고 보면 된다. mid를 (left + right) / 2를 하지 않고 left + (right - left) / 2를 하는 이유는
right값과 left 값의 합이 int형의 범위를 벗어나는 경우에 overflow가 발생하기 때문에 이를 방지하기 위함
결국 left + right/2 - left/2가 되는건데 식을 풀어보면 left/2 + right/2가 된다. (결국 동일한 식)
class Solution {
fun search(nums: IntArray, target: Int): Int {
var left = 0
var right = nums.size - 1
while (left <= right) {
var mid = left + (right - left) / 2
if (nums[mid] == target) return mid
else if (nums[mid] > target) right = mid - 1
else if (nums[mid] < target) left = mid + 1
}
return -1
}
}
Complexity Analysis
- 시간 복잡도 : O(logN)
- Space complexity : O(1) since it's a constant space solution.

- 자세한 것을 알고 싶으면 master theorem을 참고하기 바란다. 머리가 아프면 굳이 몰라도 된다. binary search는 O(logN)이다만 알고 있으면 된다!
'알고리즘 > LeetCode' 카테고리의 다른 글
| [Kotlin] Leetcode 344. Reverse String (0) | 2022.02.16 |
|---|---|
| [Kotlin] Leetcode 189. Rotate Array (0) | 2022.01.24 |
| [Kotlin] Leetcode 977. Squares of a Sorted Array (0) | 2022.01.24 |
| [Kotlin] Leetcode 35. Search Insert Position (0) | 2022.01.24 |
| [Kotlin] Leetcode 278. First Bad Version (0) | 2022.01.20 |




댓글